빅오 표기법이란?
알고리즘의 효율도를 측정하는 척도이다. 해당 알고리즘이 시간적으로 얼마나 소요되는지, 그리고 공간적으로 어느정도를 차지하는지를 알려주며, 이를 통해 알고리즘의 효율성을 파악할 수 있다. 빅오 즉, 알고리즘의 효율도를 측정하기 위한 척도는 크게 "시간복잡도"와 "공간복잡도"로 나눌 수 있다.
공간복잡도란?
공간복잡도는 안어 그대로, 프로그램을 실행시킨 후 완료하는 데 필요로 하는 자원 공간의 양을 말한다. 여기서 자원공간이라 하면, 메모리(RAM)인 것이다. 즉 해당 알고리즘을 해결하기 위해 실제로 사용되는 메모리의 양으로 효율도를 측정하는 것이고, 당연하겠지만 적게 사용될 수록 효율적임을 의미한다.
그렇다면 공간복잡도는 어떻게 계산할 수 있을까?
공간복잡도는 코드 작성 시에 선언된 변수들과 관련이 있다. 단순 변수 혹은, 고정적으로 정의된 변수는 고정공간을 차지한다. 해결하려는 문제의 특정 인스턴스에 의존하는 크기를 가진 구조화 변수들을 위해서 필요로 하는 공간, 그러니까 예를 들어 함수선언에 사용된 인자들, for문을 위한 가상의 변수들(i나 n같은)이 차지하는 공간은 가변 공간이다. 공간 복잡도는 이러한 고정공간과 가변공간의 합인 것이다.
이를 예시를 통해 살펴 보고자 한다.
|
1
2
3
|
function sample(a, b, c) {
return a + b + c * a;
}
|
cs |
a, b, c는 3개의 변수로 메모리상 1씩 3개해서 3을 차지하는 것처럼 보일 수 있지만, 외부에서 인자로 받아오고 함수는 바로 리턴하기 때문에 공간 복잡도는 0이다. 따라서 공간 복잡도는 O(1)이라고 볼 수 있다.
|
1
2
3
4
5
6
7
8
|
// arr = 배열, n = 정수
function sample(arr, n) {
let s = 0; // 1
for(let i=0; i<n; i++) { // 2;
s += arr[i]; // n
}
return s;
}
|
cs |
위 예에서는 우선 변수 s를 초기화하는 1, 그리고 i를 초기화하는 1, 그리고 for문을 끝내기 위한 n값 1, 끝으로 반복문에서 arr[i]의 n값을 해서 총 공간 복잡도는 n + 3 이 될 것이다.. 빅오 표기법으로는 O(n) 일 듯.
|
1
2
3
4
5
6
7
8
|
// n = 정수
function sample(n) {
let val = 1;
for(let i=0; i<n; i++) {
val = val * i;
}
return val;
}
|
cs |
아마도 val 이라는 변수를 초기화 하는데 1, 그리고 반복문에 사용된 변수 i에 1. 그래서 반복문이 몇번 반복되는 것과 상관 없이 공간 복잡도는 2가 되고 빅오 표기법으로는 O(1)이 될 듯.
시간복잡도란?
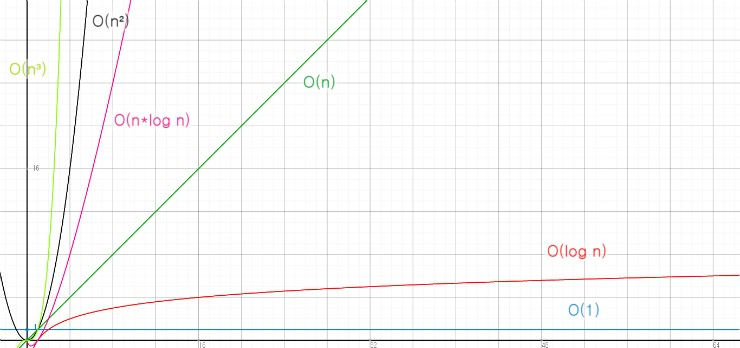
시간 복잡도는 공간 복잡도보다는 좀 더 이해하기 쉬웠다. (개념이 쉽다기 보다는 일반적으로 빅오 표기법과 시간 복잡도가 거의 한쌍처럼 같은 개념으로 같이 묶여서 많이 설명되고 사용되다보니 좀 더 익숙한 듯 하다.) 공간 복잡도가 공간의 사용에 따른 효율성을 본다면 시간 복잡도는 말 그대로 시간적인 효율성을 측정하는 것이다. 여기서 더 구체적으로 설명하자면, "시간적으로 얼마나 소요되는지"는 우리가 알고 있는 그 시간적인 개념이라기 보다는 "어떠한 알고리즘을 해결하기 위한 단계 수"이다. 그리고 보통 해당 알고리즘을 해결하기 위한 가장 최악의 단계 수를 시간복잡도로 본다. 효율성의 측면에서 성능의 순서는 상단의 그래프 이미지를 참고 하면 된다. 즉 시간 복잡도를 그래프로 표기했을 때, 가파를수록 비효율적이라는 의미이다. (해당 그래프는 공간 복잡도에도 해당되는 의미인 듯하다. 계산하는 방법은 다르지만,
결국 공간 복잡도도 빅오 표기법으로 표기 될 것이기 때문이다.)
대표적인 빅오 표기법들
O(1)
여기서 1은 숫자 1을 나타내기 보단 상수를 의미한다. 입력되는 데이터의 량과 상관없이 일정한 횟수로 실행 되거나 한 단계만을 거치는 것을 말한다. 시간이 얼마나 걸리든 한 단계만 거치면 O(1)의 복잡도를 가진다. 대표적으로 배열 끝의 삽입과 삭제의 시간복잡도가 O(1)이다.
a. 자료 구조 내의 데이터 수가 3개인 경우, 데이터 가장 앞의 요소 반환: 1번의 연산
b. 자료 구조 내의 데이터 수가 6개인 경우, 데이터 가장 앞의 요소 반환: 1번의 연산
c. 자료 구조 내의 데이터 수가 9개인 경우, 데이터 가장 앞의 요소 반환: 1번의 연산
데이터 수의 증감여부와 상관없이 연산과정은 항상 동일하다.
O(logn)
데이터의 증가량에 따라 연산 수나 단계가 늘어나지만 그 양이 n보다는 적다. 가령 n이 증가함에 따라 일정하게 시간복잡도도 비례해서 늘어나는 것이 아니라, 데이터가 n씩 증가함에 따라 시간복잡도도 증가하지만, 그 증가량에 비해 복잡도가 증가하는 양은 적다. 그러다 점차 O(1)에 가까워진다.
n 의 크기를 반씩 줄이는 걸 가정
n 이 반씩 줄다보면 k 단계에서 최종적으로 1이 된다 가정하자.
단계별로 n → n/2 → n/4 → n/2의k 승 진행
n = 2 의 k 승
양쪽에 로그 붙이면 logN = k 가 됨.
예시 : n = 16 이라 가정하면, 16 → 8 → 4 → 2 → 1 이고, 이는 logN 의 시간복잡도를 가지게 됨. 실행 횟수는 log(16) = 4 가 된다.
O(n)
데이터의 양에 따라 정비례하게 증가한다. 대표적으로 반복문을 한번 돌릴때 O(n)의 시간복잡도를 보인다.
O(nlogn)
O(n)보다는 많이 실행 되지만 O(n2)보다는 적게 실행되는 그 사이??라고 생각하면 좀 더 쉬울듯?
O(n2)
데이터에 양에 따라 걸리는 시간이 제곱에 비례하는 것을 말한다. n번 반복되는 반복문이 2번 중첩될 때를 생각하면 쉬울 것 같다.
'CS STUDY > Algorithm&Data structure' 카테고리의 다른 글
| [자료구조] Graph_1. 그래프의 개념과 특징 (0) | 2022.05.08 |
|---|---|
| 주요 DataStructure 정리_링크만첨부 (0) | 2021.02.11 |
| 재귀함수와 반복문의 차이 (0) | 2021.02.11 |
| [Python]알고리즘 문제풀이6(collections 모듈) (0) | 2021.01.20 |
| [Python]알고리즘 문제풀이 5 (0) | 2021.01.14 |